Guion de Estudios
1 Analisis de la particula
1.1 Introduccion
1.2 Concepto de fuerza, vector
1.3 Descomposicion de fuerzas en 2 y 3 dimensiones (expresion de fuerzas con vectores unitarios, cosenos directores)
1.4 Sistema de fuerzas concurrentes
1.5 Equilibrio de una particula
2 Analisis del cuerpo rigido
2.1 Fuerzas internas y externas
2.2 Principio de transmisibilidad
2.3 Diagrama de cuerpo libre
2.4 Momento de una fuerza con respecto a un punto
2.5 Momento de una fuerza con respecto a un eje
2.6 Par de fuerzas
2.7 Descomposición de una fuerza en una fuerza y un par
2.8 Sistemas equivalentes de fuerzas
2.9 Fuerzas coplanares
2.10 Fuerzas concurrentes
2.11 Restricciones al movimiento y fuerzas reactivas
2.12 Equilibrio en cuerpos rigidos sujetos a sistemas de fuerzas
2.13 Determinacion de reacciones por medio de sistemas equivalentes
3 Metodo de analisis de estructuras
3.1 Introduccion
3.2 Analisis de armadura en el plano
3.3 Analisis de marcos isostaticos
3.4 Analisis de maquinas de baja velocidad
3.5 Metodo del trabajo virtual
4 Propiedades de aereas planas y lineas
4.1. Introduccion
4.2. Primer momento de lineas y aereas (centroides y centros de gravedad de aereas por integracion y compuestas)
4.3. Segundo momento de area (simple, polar de area, teorema de ejes paralelos en 2 dimensiones, segundo momento de aereas compuestas)
5 Friccion
5.1 Friccion
5.2 Friccion seca
5.3 Leyes de friccion
5.4 Coeficientes y angulos de friccion
5.5 Analisis en planos inclinados
Hallar los vectores U y V cuyos puntos uniciales y final se dan. Mostrar que U y V son equivalentes.
U: P (3,2) Q (5,6)
V: P (-1,4) Q (1,8)

PQ = (5-3 , 6-2)
U = (2, 4)
PQ = (1+1, 8-4)
V = (2, 4)

U: P (0,3) Q (6,-2)
V: P (3,10) Q (9,5)

PQ = (6 - 0 , -2 -3)
U = (6, -5)
PQ = (9 -3, 5 -10)
V = (6, -5)

Ejemplo:
Una barca es arrastrada con dos remolcadores, si la resultante de las fuerzas ejercidas es de 5000 lb, dirigida a lo largo del eje del lanchon,
Determine la tension de cada una de las cuerdas.





Un hombre jala una cuerda atada a un edificio con una fuerza de 300N.
¿Cuales son las componentes horizontal y vertical de la fuerza ejercida en el punto A?

Resultado:
Equilibrio de la Particula
Σ F = 0
Ejemplo:

Como la particula esta en equilibrio:


Dos semaforos A y B
Si el que cuelga en B pesa 300 N, determine el peso del que cuelga en C.





Punto C


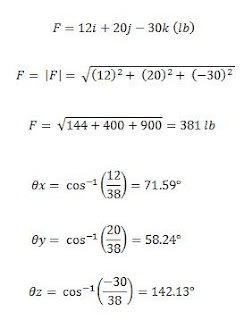
Ejemplo:
Una seccion de pared de concreto se mantiene por los cables tensados, la tension es de 840 lb en el cable AB y 1200 lb en el cable AC.
Determine la magnitud y la direccion de las resultantes ejercidas por los cables AB y AC sobre la estaca A.
A ( 16, 0, -11)
B ( 0, 8, 0)
C ( 0, 8, - 27)
Definir Segmentos
AB = -16 i + 8 j + 11 k
AC = -16 i + 8 j -16 k




Encuentre ϴx, ϴy, ϴz.



Una fuerza P de 3 lb se aplica a una palanca que controla la barrena de una barredora de nieve.
Determine el momento de P respecto a A cuando alfa es igual a 30°.

A ( 0, 0)

La tensión en la línea AB AD es de 369 N.
Determine el momento, respecto a C, de la fuerza resultante RA ejercida sobre las grúas en el punto A.




Determine el ángulo formado por los cables AB y AD.



Los elementos AB, BC y CD del marco de acero mostrado en la figura estan unidos en B y C, asegurados mediante los cables EF y EG.
Si E es el punto medio de BC y la tensión en el cable EF es de 110 lb, determine:
a) el ángulo entre EF y el elemento BC,

B (0, 16.5, 0)
C (32, 7.5, -24)
F (2, 0, 0)
E (16, 12, -12)
BC ( 32, -9, -24)
FE ( -14, -12, 12)


Una cerca consiste en postes de madera y un cable de acero sujeto a cada poste y anclado al suelo en los puntos A y D.
Si la suma de momentos, respecto al eje z, de las fuerzas ejercidas por el cable sobre los postes ubicados en B y C es de '48 lb•ft
Determine la magnitud de TDC cuando TBA = 14 lb.

A (4.5, 0, 9)
C (0, 3, 0)
D (6, 0, -6)


Una placa de acero está sometida a la acción de dos pares, según muestra la figura.
Determine:
a) el momento del par formado por las dos fuerzas de 40 N.
b) el valor de alfa si d = 820 mm, y la resultante de los dos pares es de 8 N•m en sentido contrario de las manecillas del reloj.
c) la distancia perpendicular entre las dos fuerzas de 34 N si la resultante de los dos pares.















nesecito saber el procedimiento de estos el martes tengo examen y me gustaria que publicaras los procedimientos de estos
ResponderEliminar1. Una fuerza de 90 N se aplica a la varilla de control AB como se muestra. Si la longitud de la varilla es de 225 mm, determine el momento de la fuerza respecto al punto B descomponiendo la fuerza en sus componentes a lo largo de AB y en una dirección perpendicular a AB.
MB = - 13.02 N m
2. Considerando la figura del problema 1. Una fuerza de 90 N se aplica a la varilla de control AB como se muestra. Si la longitud de la varilla es de 225 mm, determine el momento de la fuerza respecto al punto B descomponiendo la fuerza en sus componentes horizontal y vertical.
MB = - 13.02 N m
3. Una fuerza P se aplica a una palanca que controla la barrena de una barredora de nieve. Determine el momento de P respecto a A cuando = 300.
MA = 16.03 lb in
4. Considerando la figura del problema 3. Una fuerza P se aplica a una palanca que controla la barrena de una barredora de nieve. Determine la magnitud y la dirección de la fuerza P mínima que tiene un momento de 19.5 lb in en sentido antihorario respecto a A.
Pmin = 3,32 lb = - 35.30
5. Considerando la figura del problema 3. Una fuerza P de 2.9 lb se aplica a una palanca que controla la barrena de una barredora de nieve. Determine el valor de si el momento de P respecto a A es en sentido contrario a las manecillas del reloj y tiene una magnitud de 17 lb in.
= 49.90 , 59.40
6. Un rótulo está suspendido de dos cadenas AE y BF. Si la tensión en BF es de 200 N, determine a) el momento de la fuerza ejercida por la cadena en B respecto a A, b) la fuerza mínima aplicada en C que produce el mismo momento respecto a A.
MA = 386 N m Fcmin = 160.1 N = 560
7. Un rótulo está suspendido de dos cadenas AE y BF. Si la tensión en BF es de 200 N, determine a) el momento de la fuerza ejercida por la cadena en B respecto a A, b) la magnitud y el sentido de la fuerza vertical aplicada en C que produce el mismo momento respecto de A, c) la fuerza mínima aplicada en B que produce el mismo momento respecto de A.
MA = 386 N m FC = 193.2 N Fcmin = 189.5 = 78.70
loco, me sirvió muchisimo tu ejercicio de descomposición de una fuerza en 2 direc, el de
ResponderEliminar*Una barca es arrastrada con dos remolcadores...
mañana tengo parcial así que me salvaste las papas jeje, saludos desde Argentina
Gracias
LA DECOMPOSICION DE UNA FUERZA EN 2 DIMENSIONES Y TRES DIMENSIONES
ResponderEliminarSoy Артур Борис un residente/ciudadano de la República de Rusia. Tengo 52 años de edad, soy un empresario/empresario. Una vez tuve dificultades para financiar mi proyecto/negocio, si no fuera por un buen amigo mío que me presentó al Sr. Benjamin Lee para obtener un préstamo por valor de 250.000 dólares de su empresa. Cuando me puse en contacto con ellos, sólo tardé cinco días laborables en hacer el proceso de préstamo y transferirlo a mi cuenta. Incluso con un mal historial de crédito, siguen ofreciéndote sus servicios. También ofrecen todo tipo de préstamos como préstamos comerciales, préstamos para la vivienda, préstamos personales, préstamos para el coche. No sé cómo agradecerles lo que han hecho por mí, pero Dios les recompensará de acuerdo a sus riquezas en gloria. Si necesita una ayuda financiera urgente, póngase en contacto con ellos hoy mismo a través del correo electrónico 247officedept@gmail.com Información sobre WhatsApp...+1-989-394-3740
ResponderEliminarHotel Rooms & Suites - Mapyro
ResponderEliminarBook a Hotel Room & 안성 출장안마 Suite at Harrah's Las Vegas 이천 출장마사지 in 안산 출장안마 Las Vegas, NV. Make sure you check back a couple of times when you're 경기도 출장안마 at Harrah's. 원주 출장마사지